无需太多的计算,就可精确获得日月食的主要特点。日食情况是比较复杂,在地面上不同的观测位置,事件发生的时间是不同的。而对于月食,所有的观测者将在同一时刻看到相同的月相。
由于这个原因,我们将不考虑各地的日食情况。有兴趣的读者可以使用贝塞尔根计算各地的日食情况。贝塞尔根数出版在每年的《天文历书》(1981年开始更名为《天文年历》),公元-2003年到+2526年所有日食的贝塞尔根数可以在Mucke和Meeus[1]的著作中找到。Meeus[2]已发表了现代的精确的贝塞尔根数。这两本著作给出了贝塞尔根素以及他们所用的公式,并含有数值范例。
Espenak出版了一部著作[3],给出了1986到2035年的日全食(或日环食)的路径,并带有那个时期所月日食的漂亮的的世界地图。然而,这本著作不包含贝塞尔根数,所以它不提供计算额外数据的可能性,如,无法计算全食或环食路径之外的当地日食情况。
让我们提一下Stephenson和Houlden的一本著作[4],它包含了公元前1500到公元1900年可见日全食和日环食的数据及章节。
首先,利用公式(49.1)和(47.3)计算平新月和平满月时刻(JDE)。记住,对于新月(日食),k必须是一个整数,对应满月(月食),k为整数加0.5。
然后,利用公式(47.4)到(47.7)计算此时的角度M、M'、F和Ω,并利用公式(45.6)式计算E.
F的值将给出发生日食或月食的首要信息。如果F与整倍数的180度的差值小于13°.9,那么肯定要发生日月食,如果大于21°.0,那就没有日月食。如果在这两个值之间,则不能确定是否有日月食,还须进一步检查。可以使用以下规则:如果|sin F|>0.36,则没有日月食。
注意,在一个阴历月以后,F增加了30°.6705。
如果F接近0°或360°,那么日月食出现在升交点。如果F接近180度,那么食点出现在月亮轨道的降交点。计算:
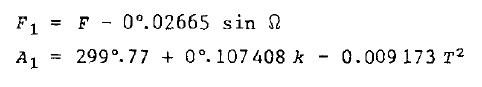
那么,要取得最大食的时间(对于地球一般是日食),使用(47.1)平会合时间加上以下修正(单位是天)。

当然,如果需要高精度,不能使用这个算法。在公元1951到2050年的221个日食,这种方法计算最大食的平均误差是0.36分钟,最大误差是1.1分。
然后计算: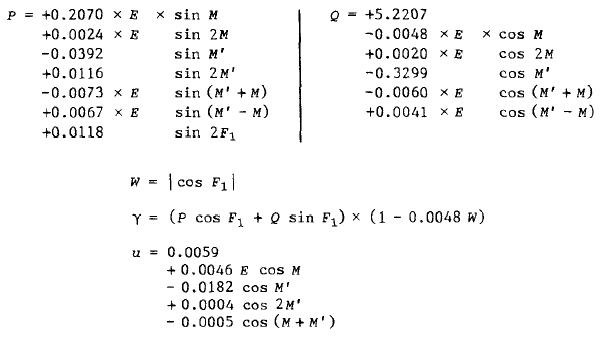
日食
在日食情况下,γ表示月影轴到地心的最小距离,单位是地球赤道半径。注意,月影轴是一条线,地心是一个点,最小距离指点到线的最小距离。当月影轴经过地心以南时,γ为正,经过地心以北时γ为负,当γ在+0.9972到-0.9972时,日食中心是:在地球表面上存在一条日食中央线,影轴在地表经过的那条线。
u表示月亮影锥在基平面上的半径,单位也是地球半径。基平面指:经过地心并且垂直月亮影轴的平面。半影锥在基平面上的半径是 u + 0.5461
如果|γ|在0.9972到1.5433+u之间,则没有日食中心,是一个部分食。不过,当|γ|在0.9972到1.0260之间的时候,影锥的一部分可能触及地表(在地球两极地区),而锥轴则没有碰到地球。当0.9972<|γ|<0.9972+|u|时,是没有中心的全食或环食(因锥轴不经过地表,所以没有中心)。在1950到2100年期间,有7次这种类型的日食:
如果|γ|>1.5433+u,在月球表面上看不到日食。
对于有中心的日食,食的类型由以下规则决定:
如果 u<0,是全食
如果 u>+0.0047,是环食
如果 u介于0到+0.0047,是环食或全环食
[注:全环食是混合食,上述的食的中心线附近的区域常称为食带,在这一食带上,有的地方是全食,有的地方即是环食,这种情况是混合食]